Previous section: Lorentz Contraction.
Next section: Lorentz Transformations.
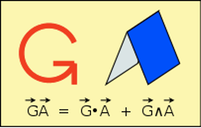
A distant source with velocity V = γ (1 + v/c) emits light signals with frequency
f ′ = ω′ / 2π = 1 / ∆t′ that are received with frequency f = ω / 2π = 1 / ∆t, as shown in the figure.
Exercise: From the figure derive the equation
λ(X2 − X1) = D − V ,
where λ is a scale factor and
D ≡ f ′ / f
is the Doppler factor. Derive and discuss the result
\[\Large{D\,\,\, = \,\,\,\frac{{f'}}{f}\,\,\, = \,\,\,\gamma \,\left( {1\,\, \pm \,\,v/c} \right)\,\,\, = \,\,\,\sqrt {\frac{{c \pm v}}{{c \mp v}}} \,\,\, = \,\,\,\frac{1}{{\gamma \,\left( {1\,\, \mp \,\,v/c} \right)}}}\]
(Click here for a solution to this exercise.)
Previous section: Lorentz Contraction.
Next section: Lorentz Transformations.